Die Laufvariable im Summenzeichen: Ein Überblick

In der Mathematik ist das Summenzeichen, dargestellt durch den griechischen Buchstaben Σ (Sigma), ein essentielles Werkzeug, um die Addition einer Vielzahl von Zahlen in einer kompakten Form zu notieren. Dabei spielt die Laufvariable eine entscheidende Rolle, da sie die Werte angibt, über die summiert wird.

Was ist eine Laufvariable?

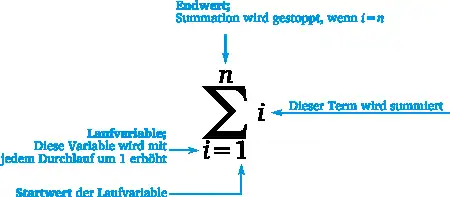
Die Laufvariable, auch als Laufindex oder Zählvariable bezeichnet, ist eine Variable, die den aktuellen Wert innerhalb einer Sequenz angibt. Sie wird typischerweise in Summen und Produkten verwendet, um die Indizes der Summanden zu definieren. Bei einer Summation, wie zum Beispiel Σ (k=1 bis n) a_k, ist k die Laufvariable, die von dem Startwert 1 bis zum Endwert n reicht.

Das Summenzeichen und seine Komponenten

Das Summenzeichen selbst besteht aus mehreren Elementen:

• Laufvariable: Die Variable, über die die Summe läuft (z.B. k)
• Startwert: Die untere Grenze der Laufvariable (z.B. 1)
• Endwert: Die obere Grenze der Laufvariable (z.B. n)
• Funktionswert: Der Ausdruck, der in der Summe berechnet wird (z.B. a_k)

Beispiele zur Veranschaulichung

Um die Anwendung der Laufvariable besser zu verstehen, schauen wir uns einige Beispiele an:

Beispiel 1: Berechnung der Summe von Quadratzahlen

Berechne die Summe Σ (k=1 bis 5) k^2.

1. Bestimme die Laufvariable: k
2. Setze den Startwert: 1
3. Setze den Endwert: 5
4. Berechne die Funktionswerte:
• k=1: 1^2 = 1
• k=2: 2^2 = 4
• k=3: 3^2 = 9
• k=4: 4^2 = 16
• k=5: 5^2 = 25
5. Addiere die Funktionswerte: 1 + 4 + 9 + 16 + 25 = 55

Beispiel 2: Eine lineare Summe

Berechne die Summe Σ (i=5 bis 8) 3i.

1. Startwert: 5
2. Endwert: 8
3. Funktionswerte:
• i=5: 3*5 = 15
• i=6: 3*6 = 18
• i=7: 3*7 = 21
• i=8: 3*8 = 24
4. Addiere die Ergebnisse: 15 + 18 + 21 + 24 = 78

Regeln für das Arbeiten mit dem Summenzeichen

Wenn du mit dem Summenzeichen arbeitest, gibt es einige wichtige Regeln, die du beachten solltest:

• Konstante Faktoren: Du kannst konstante Faktoren vor das Summenzeichen ziehen.
• Aufspalten von Summen: Eine Summe kann in mehrere Teile aufgeteilt werden.
• Indexverschiebung: Die Grenzen der Laufvariable können verändert werden, indem du den gesamten Index um einen konstanten Wert verschiebst.

Häufige Fehler im Umgang mit dem Summenzeichen

Um Fehler zu vermeiden, solltest du dir einige häufige Missverständnisse vor Augen führen:

• Die Summe von Produkten ist nicht gleich dem Produkt der Summen.
• Ein Exponent kann nicht aus der Summe herausgezogen werden.

Fazit

Die Laufvariable ist ein zentrales Element beim Arbeiten mit dem Summenzeichen. Sie ermöglicht es, Summen klar und präzise darzustellen und zu berechnen. Ein fundiertes Verständnis der Laufvariable und ihrer Verwendung ist entscheidend für erfolgreiches Arbeiten in der Mathematik und Informatik.

Für weitere Informationen über Programmierkonzepte und deren Anwendung in der Praxis, schau dir unseren Artikel über Die for-Schleife in Python: Grundlagen und Anwendungen an.